As a developer, you've probably encountered the challenge of string matching. Whether you're building a spell checker, fuzzy search engine, or trying to compare strings in your database, exact matches aren't always enough—especially when dealing with typos or OCR-generated text.

In this article, we’ll explore practical methods for approximate string matching using Python. We’ll cover:

• Three popular metrics for string similarity: Jaccard distance, Longest Common Substring, and Levenshtein distance.
• How to leverage Python libraries like difflib, fuzzywuzzy, and regex.
• Code examples you can adapt to your own language of choice.

Metrics for Effective String Comparison

String matching often depends on comparing how similar two strings are, even when they're not exactly alike.

Choosing the right similarity metric depends on your context: do you care about speed, accuracy, or tolerance to typos?

There are plenty of ways for measuring string similarity but we will be discussing these below:

• The Jaccard distance, great for quick, set-based comparison.
• The longest common substring percentage, useful when character order matters.
• The Levenshtein similarity (that can also be used to calculate confidence score), best for typo-tolerance and edit tracking.

The choice of metric for string comparison largely depends on the specific requirements of your application.

For instance, if you are dealing with large datasets where performance is critical, simpler methods like Jaccard distance may be preferred due to their speed.

However, if accuracy is important, especially in cases where character order and typographical errors are significant, more sophisticated approaches like Levenshtein similarity or the longest common substring percentage may be more appropriate.

Understanding the strengths and weaknesses of each method will help you select the most suitable one for your string matching needs!

The Jaccard Distance

One of the simplest methods for measuring similarity between two sets of elements is to use the Jaccard distance.

Essentially, it calculates the ratio of the count of unique characters that appear in both strings to the total count of unique characters that are found in either of the two strings. This ratio provides a clear numerical representation of how similar or different the two strings are based on their unique character contributions.

Here is the implementation of the Jaccard distance in Python:

def jaccard_similarity(s1: str, s2: str)->float:
	"""Computes the Jaccard similarity score between s1 and s2."""
	return len(set(s1) & set(s2)) / len(set(s1) | set(s2))

if __name__ == "__main__":
	s1 = "String matching is not easy"
	s2 = "Compare two strings is not easy"
	jaccard_sim = jaccard_similarity(s1, s2)
	print(f"The Jaccard similarity between {s1} and {s2} is {jaccard_sim}")

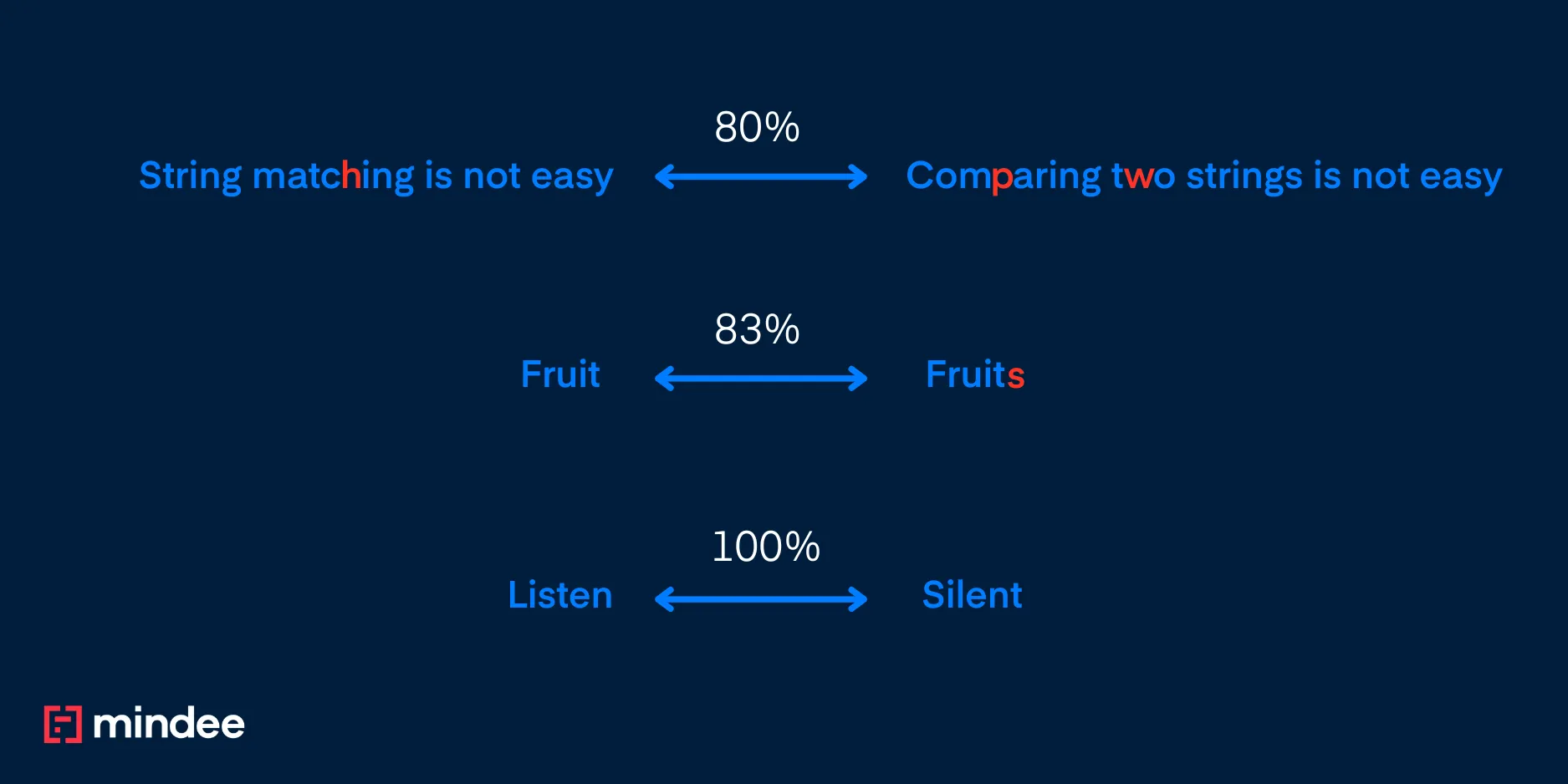
For example, the Jaccard similarity between “fruit” and “fruits” is 5/6.

How effective is this metric, you might ask? It is actually fairly simple and easy to implement, which makes it quite appealing for various applications. However, one significant limitation is that it does not consider the order in which the characters appear.

For example, the Jaccard distance between SILENT and LISTEN is …… 1 – 6/6 = 0. So we need something more robust.

The Longest Common Sub-string Percentage

The longest common substring refers to the longest sequence of characters that can be found in both of the given strings.

To visualize this concept, consider two strings, which could be sequences of letters or numbers, and determine the segment of characters that they share in common, and is the longest in length. This idea leads us to a way to measure how similar the two strings are by calculating the ratio.

This ratio is determined by dividing the length of that longest common substring by the shorter of the two strings' lengths. This approach gives us insight into how closely related the strings are to each other based on the characters they contain.

So in the examples above:

• “Fruit” and “Fruits” gives 100% score as the full word “Fruit” is the longest common substring and
• “Listen” and “Silent” gives 1/3 , as two characters (”en”) out of six are common

Depending on your use case, you can also compute the ratio using the maximum length from both strings:

• Using minimum length: A score of 100% means that one of the two strings is completely included in the other.
• Using maximum length: A score of 100% is possible only when the two strings are exactly the same.

Here is a python implementation of this method using difflib:

from difflib import SequenceMatcher

def longest_common_substring(s1: str, s2: str) -> str:
		"""Computes the longest common substring of s1 and s2"""
    seq_matcher = SequenceMatcher(isjunk=None, a=s1, b=s2)
    match = seq_matcher.find_longest_match(0, len(s1), 0, len(s2))

    if match.size:
        return s1[match.a : match.a + match.size]
    else:
        return ""

def longest_common_substring_percentage(s1 : str, s2 : str) -> float:
	"""Computes the longest common substring percentage of s1 and s2"""
	assert min(len(s1), len(s2)) > 0, "One of the given string is empty"
	return len(longest_common_substring(s1, s2))/min(len(s1), len(s2))

However, what happens if I want to compare “goodbye” and “goozbye”? Well, the longest common substring is “goo” so the similarity would be 3/7 which is very low given that only one character differs.

Levenshtein Similarity

The Levenshtein distance is a concept used to measure how different two strings are from each other. Specifically, it calculates the minimum number of changes that must be made to one string in order to transform it into another string.

These changes can include actions such as inserting a character, deleting a character, or substituting one character for another.

By counting these changes, the Levenshtein distance provides a numerical value that represents the level of dissimilarity between the two strings being compared.

The Levenshtein distance is actually a specific instance of a broader category known as EDIT distance.

While the Levenshtein distance assigns a uniform weight of 1 to each type of modification—meaning that every insertion, deletion, or substitution counts the same—EDIT distance in general allows for different weights to be assigned to different types of modifications.

This means that in the case of EDIT distance, you can prioritize some changes as being more significant than others, allowing for a more nuanced comparison between strings.

So in the examples above:

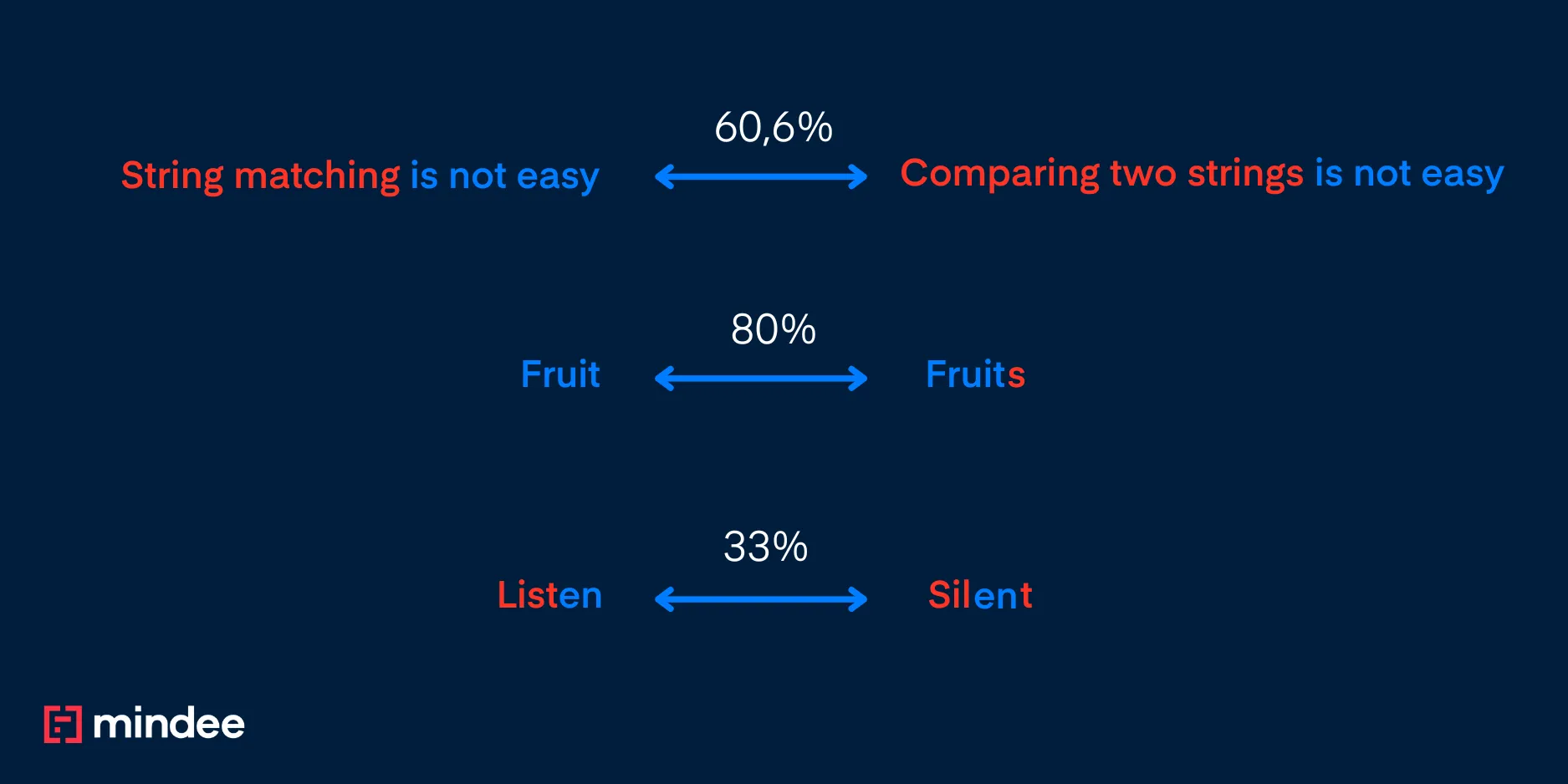
• “Fruit” and “Fruits” gives an 80% score as one error is introduced by ‘s’ out of five characters for the smallest word, hence 1-(1/5) being 80%
• “Listen” and “Silent” gives 33% as the minimal number of operations to make them match is 4 with two replacement needed, one insertion and one deletion, hence 1-(4/6) being 33%

The EDIT distance gives more flexibility because it’s possible to fine-tune the weights in order to fit your problem better.

A modification can be of 3 types:

• Insert: Add an extra character
• Delete: Delete a character
• Replace: Replace a character

NB: Sometimes, the Replace modification is not used and is considered as a deletion plus an insertion. You can also find some definitions including the Transposition modification.

To get a comparison score from the Levenshtein distance as on the other methods, we can divide the distance by either the length of the shortest string or the longest string.

s1 = "listen"
s2 = "silent"
[('replace', 0, 0), ('delete', 2, 2), ('replace', 3, 2), ('insert', 6, 5)]

s1 = "fruit"
s2 = "fruits"
[('insert', 5, 5)]

s1 = "string matching is not easy"
s2 = "compare two strings is not easy"

[('insert', 0, 0), ('insert', 0, 1), ('insert', 0, 2), ('replace', 0, 3), ('replace', 1, 4), ('replace', 3, 6), ('replace', 4, 7), ('replace', 5, 8), ('replace', 6, 9), ('replace', 7, 10), ('replace', 8, 11), ('replace', 9, 12), ('replace', 10, 13), ('replace', 11, 14), ('insert', 15, 18)]

# forget about the spacing 
string matching is not easy               # source string 
**c**string matching is not easy              # 1 - insert 'c'
c**o**string matching is not easy             # 2 - insert 'o'
co**m**string matching is not easy            # 3 - insert 'm'
com**p**tring matching is not easy            # 4 - replace 's' with 'p'
comp**a**ring matching is not easy            # 5 - replace 't' with 'a'
compar**e**ng matching is not easy            # 6 - replace 'i' with 'e'
compare **t**g matching is not easy           # 7 - replace 'n' with 't'
compare t**w** matching is not easy           # 8 - replace 'g' with 'w'
compare tw**o** atching is not easy           # 9 - replace 'm' with 'o'
compare two **s**tching is not easy           # 10 - replace 'a' with 's'
compare two sthing is not easy            # 11 - delete 'c'
compare two st**r**ing is not easy            # 12 - replace 'h' with 'r'
compare two string**s** is not easy           # 13 - insert an 's'

Here is an implementation of a comparison score using Levenshtein distance:

from Levenshtein import distance
def levenshtein_distance_percentage(s1: str, s2: str) -> float:
    """Computes the Levenshtein dis"""
    assert min(len(s1), len(s2)) > 0, "One of the given string is empty"
    return 1. - distance(s1, s2) / min(len(s1), len(s2))

‍

How to Search Allowing Mistakes Using Regular Expressions?

The package regex in Python allows searching using regular expressions that allow fast search in text data. This package has a powerful feature that allows partial regex matching. We will introduce this feature and give a taste of its power in the following paragraph.

Approximate Matching with Regex

Regexes are used to define a search pattern and allow to find matches inside strings. The use of approximate matching is possible using packages like regex in python: it can allow the search for a pattern with some acceptable errors.

The regex library's approximate matching capabilities are particularly useful in scenarios where data may be imperfect or contain errors, such as in OCR outputs.

By allowing for a certain degree of flexibility in the search patterns, developers can effectively retrieve relevant information even when the input strings are not exact matches. This feature is invaluable in applications like text analysis, data cleaning, and natural language processing, where the ability to account for variations and mistakes can significantly enhance the accuracy and reliability of results.

You may be interested in searching keywords in a scanned document having OCR errors.

In fact, OCR errors can show some recurring patterns (like the following: “w” → (“vv” or “v”), “O” → “0” , “y” → “v”), hence by allowing some maximum number of errors or by specifying the type of errors allowed (insertion, deletion, substitution) we can find those keywords, as in the examples below:

import regex

# search pattern for key word way
ptrn = "(?:way){e<=2:[v]}"

regex.findall(ptrn, "it is way better") 
['way']

regex.findall(ptrn, "it is wav better") 
['wav']

regex.findall(ptrn, "it is vvay better")
['vvay']

regex.findall(r"\\b(?:w{1s+1i<=2:[v]}ay)\\b", "it is vvay better")  
['vvay']

The identifier for allowing general errors is : {e} , by doing this we are not specifying how many errors are tolerated, hence to put an upper limit to the number of errors we will use the sign “≤”, for example, an upper limit of two errors we will use {e≤=2}.

Moreover, we can specify the character introducing the error, which can be introduced by substitution/insertion forming the error, by using this identifier {e<=2:[v]}.

The upper limit for the number of errors can be more specified, as we can specify it by error type, as in the last example above: we wanted the sum of the number of substitutions and number of insertions not to exceed 2, resulting in this identifier {1s+1i<=2:[v]}.

You can also take a look at our article on how to build AI products!

Conclusion

As we have observed, there are numerous techniques available for conducting approximate search and matching in various contexts. These techniques can vary widely in complexity:

‍

On one end of the spectrum, we have simpler methods like Jaccard distance, which provides a straightforward way to measure similarity between sets.

On the other end, we encounter more sophisticated approaches, such as Levenshtein similarity, which calculates the minimum number of single-character edits required to change one string into another.

Additionally, these methods can be effectively utilized in conjunction with regular expressions through the Python regex library. This integration enables users to perform fast and efficient searches within textual data, making it easier to locate patterns and match strings according to specific criteria.